Data Structures and Coding Mini-blog
This is a new part of the website that I am using to (hopefully) revive my interest in data structures and coding! This is not meant to teach comprehensively- it's more of practice to help me better understand data structures and other concepts for review, so certain concepts may not be explained very well
Radix Sort
Although I have yet to implement this sorting method, the ideas are elementary enough conceptually that I can appreciate! The radix sort is implemented by sorting elements by the increasing sequence of their integer values per digit. Although it seems limited in its comparison of integer, this type of sorting can be used for non-integer types of data through hashing. This sorting starts by evaluating the highest digit place of each element. With the example array [485, 243, 973, 5, 43, 44], we can see that the largest number of digits in a single element is 3 (for example, 483 has 3 digits). The digit count can be found by finding the largest value in the array; A simple for-loop can compare the sizes of values and assigns a max variable to the largest value until the iteration is complete.
We will then sort the elements in the array by the ones place first, tens place next, then hundreds place last. For elements with less than three digits, we can use 0 in place of the hundreds. The revised (unsorted) array would look like [485, 243, 973, 005, 043, 044].
| Radix Sort Example | Steps |
|---|---|
| [485, 243, 973, 005, 043, 044] | unsorted array |
| [043, 243, 973, 044, 485, 005] | sort by one |
| [005, 043, 243, 044, 973, 485] | sort by tens |
| [005, 043, 044, 243, 485, 973] | sort by hundreds |
| [005, 043, 044, 243, 485, 973] | sorted array |
Huffman Algorithm
Huffman algorithm is a code that utilizes binary, dealing with 0s and 1s only. It is a way to compress data in a space efficient and lossless way by assigning a certain binary combination. We create a binary tree with each unique character assigned to a node. The more often a symbol is present in the set, the higher up the symbol is placed in the tree. The binary combination is determined by the path we connect from the root to the node representing the symbol through the edges. The left edge represents 0 and the right represents 1.
I find that huffman coding is very fun to draw out, it's almost like a "choose your own adventure" puzzle*. As an example, I will sort the string "fluffy". The char 'f' appears 3 times, while the rest are only present once. This creates potential for variation in building the tree itself.
*It's possible to get different trees compression rates for the same input because chracters with the same frequency can be interchangeable when initially ordered.
| 'u':1 | 'y':1 | 'l':1 | 'f':3 |
|---|---|---|---|
I've taken the liberty of sorting the set of the symbols in increasing frequency, because this will be crucial in our next step (another important step is to include " " if it is present in the set, which can sometimes be overlooked!). After we have established this initial array, we can start to build the tree from the bottom. We make the first two elements children that connect to a parent node assigned "", assign the parent node with the added frequencies of its children (1+1), then sort the array again.
| 'y':1 | "":2 | 'f':3 |
|---|---|---|
Repeat the steps until we get to one element. This is such a small string and does not demonstrate this, so I'll note that the following steps add the next two smallest frequencies, which could mean that the following children set do not directly connect to the preceding combination of nodes in the process if the length of the string is long enough.
| "":3 | 'f':3 |
|---|---|
| "":6 |
|---|
The final representation of the tree might look like this:
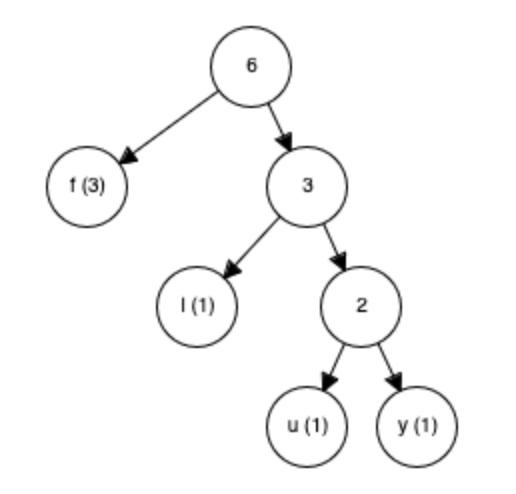
image source (and great visualization resource!):https://cmps-people.ok.ubc.ca/ylucet/DS/Huffman.html
These lines connecting each node called edges are the next step in creating the binary combinations. Starting from the root, we can make our way to each node- 'f' takes one edge, while 'y' takes three. To reiterate, the left edges represent 0 and the right represent 1. Each time we go through an edge, we add a bit (0/1) to the code that represents each symbol. Thus,
f:0
l:10
u:110
y:111
The beauty in huffman coding is the efficiency of the binary combination assignments. Since the character f is present the most often, it makes sense that it is assigned a binary representation that is the smallest. Otherwise, the compression would not be as optimal for space and speed of travel. The final binary representation of the string "fluffy" would be transformed into 01011000111!
B-Trees
B-Trees are sorted search trees that have the same height for each leaf, making them balanced. The right child nodes are larger than the parent nodes, and the left are smaller thus can be read in ascending order with in order traversals (LMR), similar to BSTs. Unlike a binary search tree however, they can have more than two children and can store multiple keys in a single node; thus, the height is reduced significantly for faster searching. The keys also have to be stored in sequential (increasing) order and include a boolean value that states itself true if it is a leaf node in the larger structure.
They are often mentioned as a data structure that is present in secondary storage devices, such as hard disk drives and solid state drives because of the need for fast searching in large spaces. This is better for locality, which is the concept of having data physically closer to the device unit that processes the information. This increases accessibility speed, thus improving the performance of transferring data (latency).
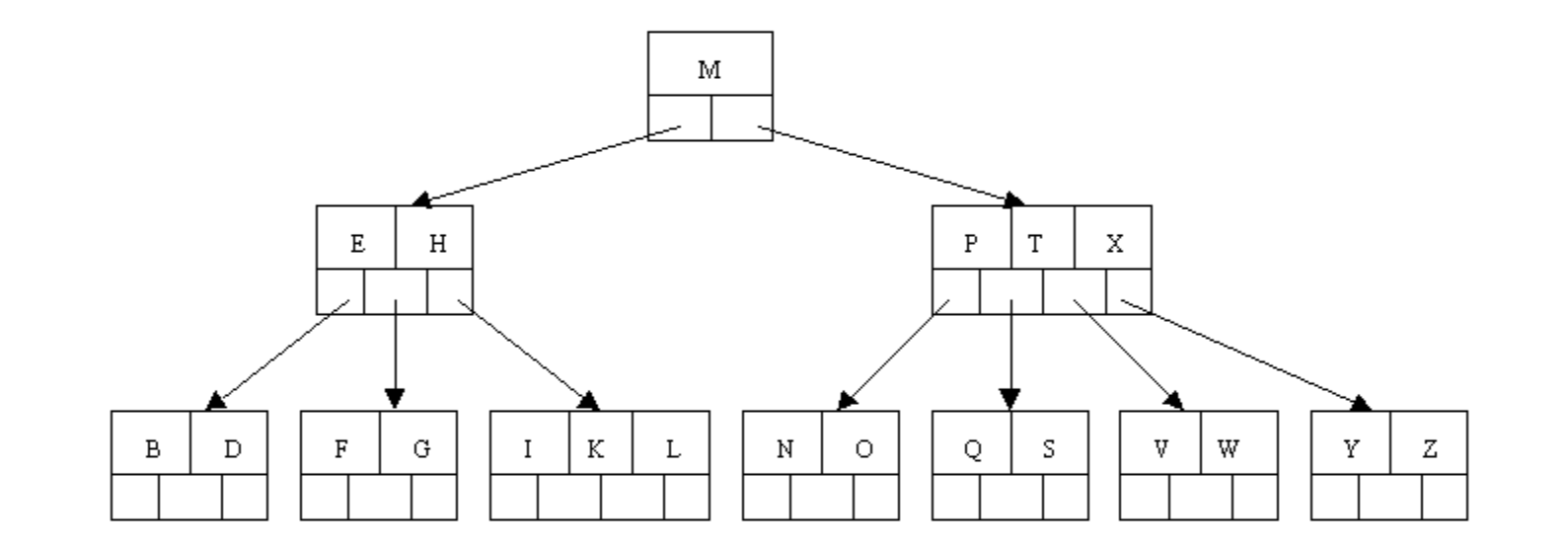
image source:https://cis.stvincent.edu/html/tutorials/swd/btree/btree.html
The tree above represents an example of a B-tree. M represents the maximum number a node can hold. Each leaf node has to contain half the nodes of m with the ceiling function applied (ceil(m/2)), or in other words at least half of the maximum number of child nodes.